MathJax is pretty much the same as Latex.
I'll email you the text I used for the first comment.
Tuesday, February 27, 2018
HW 7a -graphene. Due Wednesday night
"Unfortunately, no one can be told what the Matrix is. You have to see it for yourself." Morpheus
1. a) Using the matrix we derived in class today, find the energy of the 2pz orbital-related states in graphene as a function of \(k_y\), for \(k_x=0\). That is, calculate and graph \(E_\vec{k}\) along the \(k_y\) axis from (0,0) to the edge of the Brillouin zone. (You can assume that the hoping integral is about -2 eV.
extra credit. Why can we assume that the hopping integral, \(\gamma\), is negative in this case?
b) Where (that is, at what value of \(k_y\), is the edge of the Brillouin zone along ky? (post here in a comment or email me when you get to this.) (no derivation or shown work needed. Just the answer. (Which will be proportional to like \(\pi/b\), right?)
c) extra credit. (This is an interesting question, not just a throwaway.) What sort of information do you get if you keep going along the \(k_y\) axis past the edge of the 1st BZ? What do you learn from that?? hint: Draw the pattern of BZ's in k space. (thinking outside the box...)
2. extra credit. Suppose you would wish to calculate the dispersion relation for graphene from \(\Gamma\) to K to M and back to \(\Gamma\). Which parts of that can you do using the above matrix? Which part can you not do without considering a non-zero \(k_x\)? hint: use symmetry.
3. extra credit. What are the eigenvectors for the two branches of \(E_\vec{k}\) along the \(k_y\) axis?
4. deep extra credit. What are the eigenvectors for the two branches of \(E_\vec{k}\) along the \(k_x\) axis?
-see below for Matrix and Video
1. a) Using the matrix we derived in class today, find the energy of the 2pz orbital-related states in graphene as a function of \(k_y\), for \(k_x=0\). That is, calculate and graph \(E_\vec{k}\) along the \(k_y\) axis from (0,0) to the edge of the Brillouin zone. (You can assume that the hoping integral is about -2 eV.
extra credit. Why can we assume that the hopping integral, \(\gamma\), is negative in this case?
b) Where (that is, at what value of \(k_y\), is the edge of the Brillouin zone along ky? (post here in a comment or email me when you get to this.) (no derivation or shown work needed. Just the answer. (Which will be proportional to like \(\pi/b\), right?)
c) extra credit. (This is an interesting question, not just a throwaway.) What sort of information do you get if you keep going along the \(k_y\) axis past the edge of the 1st BZ? What do you learn from that?? hint: Draw the pattern of BZ's in k space. (thinking outside the box...)
2. extra credit. Suppose you would wish to calculate the dispersion relation for graphene from \(\Gamma\) to K to M and back to \(\Gamma\). Which parts of that can you do using the above matrix? Which part can you not do without considering a non-zero \(k_x\)? hint: use symmetry.
3. extra credit. What are the eigenvectors for the two branches of \(E_\vec{k}\) along the \(k_y\) axis?
4. deep extra credit. What are the eigenvectors for the two branches of \(E_\vec{k}\) along the \(k_x\) axis?
-see below for Matrix and Video
Monday, February 26, 2018
kinetic energy expectation value
this post is related to things we will cover in the future.
I think that for H2+ the integrand for the kinetic energy expectation value is:
\( \psi_m (\vec{r})(\frac{-\hbar^2}{2m})\bigtriangledown^2 \psi_m (\vec{r})\)
where,
\( \psi_m( \: \vec{r}) = \frac{c_m(b)}{\sqrt{2}} ( \psi_{1s} (r) + \psi_{1s}(\:\vec{r}-b \hat{x})) \)
where b is the distance between the two protons.
Note that \(c_m(b)\) is a function of b, is close to 1 for most values of b, and is unit-less. It has to be evaluated by a normalization integral for each value of b.
Also, one can turn hbar^2/m into a simple fixed number, which is easier to use in numerical calculation, using:
\(\hbar^2/m = .076 \:eV nm^2\)
I think that for H2+ the integrand for the kinetic energy expectation value is:
\( \psi_m (\vec{r})(\frac{-\hbar^2}{2m})\bigtriangledown^2 \psi_m (\vec{r})\)
where,
\( \psi_m( \: \vec{r}) = \frac{c_m(b)}{\sqrt{2}} ( \psi_{1s} (r) + \psi_{1s}(\:\vec{r}-b \hat{x})) \)
where b is the distance between the two protons.
Note that \(c_m(b)\) is a function of b, is close to 1 for most values of b, and is unit-less. It has to be evaluated by a normalization integral for each value of b.
Also, one can turn hbar^2/m into a simple fixed number, which is easier to use in numerical calculation, using:
\(\hbar^2/m = .076 \:eV nm^2\)
Sunday, February 25, 2018
Energetics of bonding.
This post is related to things we will cover in the future.
added: You can use this:
\(e^2/(4 \pi \epsilon_o) = 1.44 \:eV nm\)
Also, here is another useful relationship:
\(\hbar^2/m = .076 \:eV nm^2\)
This post is about the energetics of chemical bonding. Why would 2 nitrogen atoms in the air prefer to be in the form of N2? Or why would two hydrogen atoms prefer to be paired, to form H2, rather than remaining separate? Additionally, what determines the distance between the two nuclei in a molecule like N2 or H2? Perhaps we can learn about the fundamental origin of bonding and of bond length by looking at the simplest case, H2+. I think studying that will help us understand the energetics of sp2 bonding as well.
H2+ involves two protons and one electron. I believe we can write the wave equation for that as:
\(\frac{-\hbar^2}{2m} \bigtriangledown^2 \psi(\vec{r}) +[ \frac{-e^2}{4 \pi \epsilon_{o} r} + \frac{-e^2}{4 \pi \epsilon_{o} \:(\vec{r}-b \hat{x})}] \:\psi(\vec{r}) = E \:\psi(\vec{r}) \),
where the first term is the kinetic energy term for our one electron, and the 2nd term is the potential energy of the electron-proton interactions (two protons). b is the distance between the two protons. We don't know what that should be, but we can vary b to find out how to get the lowest energy.
Finding the exact ground state wave-function for the above wave equation is very challenging, but suppose we try an intuitive molecular state of the form,
\( \psi_m( \: \vec{r}) = \frac{c_m}{\sqrt{2}} ( \psi_{1s} (r) + \psi_{1s}(\:\vec{r}-b \hat{x})) \)
where b is, again. the distance between the two protons. Note that \(c_m\) is a function of b, is close to 1 for most values of b, and is unit-less. It has to be evaluated by a normalization integral for each value of b. (added 2-26-18)
\(\psi_{1s} (\vec{r}) = \frac{1}{\sqrt{\pi a^3}} e^{-r/a}\)
is the atomic ground state, with a fixed at .053 nm (the Bohr radius).
So then \(\psi_{1s}(\:\vec{r}-b \hat{x}))= \frac{1}{\sqrt{\pi a^3}} e^{-\sqrt{(x-b)^2 + y^2 +z^2)}/a} \)
So then the total potential energy of this system of three objects would consist of:
1) the proton-proton repulsion, which is simply \(U_{p-p} = \frac{+e^2}{4 \pi \epsilon_{o}b}\) and,
2) the expectation value of the electron-proton interaction potential energy. That involves an integral of the wave function squared over 3d space, right? I think the integrand for that may be:
\( \psi_m (\vec{r}) [ \frac{-e^2}{4 \pi \epsilon_{o} r} + \frac{-e^2}{4 \pi \epsilon_{o} \:(\vec{r}-b \hat{x})}] \:\psi_m (\vec{r})\)
So there is a positive potential energy associated with the proton-proton repulsion, and a negative potential energy associated with electron proton attraction. So we wonder: which one is bigger? How much bigger would it have to be to justify bonding? How do they depend on b, the separation between the two protons (and the parameter that appears in both the repulsive and attractive potential energy terms)?
Bottom line:Could someone calculate this for a few values of b and see what you get. Like say b = 1.5a, 2a and 2.5a, where a is the fixed Bohr radius, 0.053 nm.
Better: Just input a as a fixed value, .053 nm, and calculate for b values of:
0.06 nm, 0.08 nm, 0.10 nm, 0.12nm, 0.14 nm and 0.16 nm.
See what you get with that.
added: You can use this:
\(e^2/(4 \pi \epsilon_o) = 1.44 \:eV nm\)
Also, here is another useful relationship:
\(\hbar^2/m = .076 \:eV nm^2\)
This post is about the energetics of chemical bonding. Why would 2 nitrogen atoms in the air prefer to be in the form of N2? Or why would two hydrogen atoms prefer to be paired, to form H2, rather than remaining separate? Additionally, what determines the distance between the two nuclei in a molecule like N2 or H2? Perhaps we can learn about the fundamental origin of bonding and of bond length by looking at the simplest case, H2+. I think studying that will help us understand the energetics of sp2 bonding as well.
H2+ involves two protons and one electron. I believe we can write the wave equation for that as:
\(\frac{-\hbar^2}{2m} \bigtriangledown^2 \psi(\vec{r}) +[ \frac{-e^2}{4 \pi \epsilon_{o} r} + \frac{-e^2}{4 \pi \epsilon_{o} \:(\vec{r}-b \hat{x})}] \:\psi(\vec{r}) = E \:\psi(\vec{r}) \),
where the first term is the kinetic energy term for our one electron, and the 2nd term is the potential energy of the electron-proton interactions (two protons). b is the distance between the two protons. We don't know what that should be, but we can vary b to find out how to get the lowest energy.
Finding the exact ground state wave-function for the above wave equation is very challenging, but suppose we try an intuitive molecular state of the form,
\( \psi_m( \: \vec{r}) = \frac{c_m}{\sqrt{2}} ( \psi_{1s} (r) + \psi_{1s}(\:\vec{r}-b \hat{x})) \)
where b is, again. the distance between the two protons. Note that \(c_m\) is a function of b, is close to 1 for most values of b, and is unit-less. It has to be evaluated by a normalization integral for each value of b. (added 2-26-18)
\(\psi_{1s} (\vec{r}) = \frac{1}{\sqrt{\pi a^3}} e^{-r/a}\)
is the atomic ground state, with a fixed at .053 nm (the Bohr radius).
So then \(\psi_{1s}(\:\vec{r}-b \hat{x}))= \frac{1}{\sqrt{\pi a^3}} e^{-\sqrt{(x-b)^2 + y^2 +z^2)}/a} \)
So then the total potential energy of this system of three objects would consist of:
1) the proton-proton repulsion, which is simply \(U_{p-p} = \frac{+e^2}{4 \pi \epsilon_{o}b}\) and,
2) the expectation value of the electron-proton interaction potential energy. That involves an integral of the wave function squared over 3d space, right? I think the integrand for that may be:
\( \psi_m (\vec{r}) [ \frac{-e^2}{4 \pi \epsilon_{o} r} + \frac{-e^2}{4 \pi \epsilon_{o} \:(\vec{r}-b \hat{x})}] \:\psi_m (\vec{r})\)
So there is a positive potential energy associated with the proton-proton repulsion, and a negative potential energy associated with electron proton attraction. So we wonder: which one is bigger? How much bigger would it have to be to justify bonding? How do they depend on b, the separation between the two protons (and the parameter that appears in both the repulsive and attractive potential energy terms)?
Bottom line:
0.06 nm, 0.08 nm, 0.10 nm, 0.12nm, 0.14 nm and 0.16 nm.
See what you get with that.
Saturday, February 24, 2018
HW 6b (graphene). due Monday night.
(or, I guess Tuesday morning would be okay)
1. Considering graphene, suppose you are given the (x,y) positions of two carbon atoms. One is at (0,0) and the other is at (b,0). (Aside: b = .142 nm I think.)
a) do a drawing that shows these two atoms and all the nearest neighbors of these two atoms. (how many are there. email that to me as soon as you work on this!)
b) calculate all atom to atom distances in your drawing. (how many are there. email that to me as soon as you work on this!)
b') extra credit. What are the Bravais lattice generating vectors for the graphene lattice structure?
c) Find the location of the "first Brillouin boundary" along the ky axis. (There will be a spot along the +ky axis and another point, mirroring that, along the -ky axis.) Where exactly is that relative to like \(\pi/b\)? (email that to me ) (Feel free to use online resources for this. It is not that easy. Just so long as you get the answer as it applies to our lattice orientation and lattice parameter, b.)
d) extra credit. Find the location of the "first Brillouin boundary" along the kx axis. (There will be a spot along the +kx axis and another point, mirroring that, along the -kx axis.) Where exactly is that relative to like \(\pi/b\)?
b') extra credit. What are the Bravais lattice generating vectors for the graphene lattice structure?
c) Find the location of the "first Brillouin boundary" along the ky axis. (There will be a spot along the +ky axis and another point, mirroring that, along the -ky axis.) Where exactly is that relative to like \(\pi/b\)? (email that to me ) (Feel free to use online resources for this. It is not that easy. Just so long as you get the answer as it applies to our lattice orientation and lattice parameter, b.)
d) extra credit. Find the location of the "first Brillouin boundary" along the kx axis. (There will be a spot along the +kx axis and another point, mirroring that, along the -kx axis.) Where exactly is that relative to like \(\pi/b\)?
e) extra credit. What is the shape of the first Brillouin zone (BZ)? (Note. Make sure you find the BZ for our orientation of the spatial lattice, that is, with an atom-pair bond parallel to the spatial x axis, not the y axis.)
2. Major extra credit project problem!
Calculate the hopping integral, gamma, associated with an electron in the 2pz state on one lattice site hopping to the 2pz orbital on an adjacent site. For example, I think the integrand could be:
\(\psi_{2pz}(\:\vec{r}) \: \frac{4e^2}{4 \pi \epsilon_{o} \epsilon r} \: \psi_{2pz}(\:\vec{r}-b \hat{x})\). Does that integrand look correct? Do the units work out? Over what region would you integrate? (You can email me to discuss if your would like to work on this.) (We can use this result in our band structure calculation for the 2pz band of graphene.)
Friday, February 23, 2018
Expectation value calculations
This models how one can break a complex problem into parts and thereby make it less daunting. Additionally, I think breaking this problem into parts can reduce the likelihood of mathematical errors, and/or it can help you isolate where the errors may be!
Thursday, February 22, 2018
Class February 22
Consider an electron in the state:
\(\sqrt{1/3}\:\psi_{2s} - \sqrt{1/6}\:\psi_{2px} + \sqrt{1/2}\:\psi_{2py} \)
This is a normalized, one-electron state. Let's calculate the x and y components of the expectation value of the position of that electron.
---------------------------------------------------------
Today we calculated the expectation values for <x> and <y>. We found out that they both have integrals that are equal to the same value. However, they are different values. They depend on A, the normalization factor, and the coefficients(sqrt(1/3), sqrt(1/6), and sqrt(1/2)). Most terms cancelled out though.
For <x> the term that didn't turn to zero was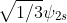(\sqrt{1/6}\psi&space;_{2px}))
For <y> the term that didn't go to zero was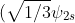(\sqrt{1/2}\psi&space;_{2py}))
Work done for <x>


Work done for <y>

Answers to both <x> and <y> expectation values

\(\sqrt{1/3}\:\psi_{2s} - \sqrt{1/6}\:\psi_{2px} + \sqrt{1/2}\:\psi_{2py} \)
This is a normalized, one-electron state. Let's calculate the x and y components of the expectation value of the position of that electron.
---------------------------------------------------------
Today we calculated the expectation values for <x> and <y>. We found out that they both have integrals that are equal to the same value. However, they are different values. They depend on A, the normalization factor, and the coefficients(sqrt(1/3), sqrt(1/6), and sqrt(1/2)). Most terms cancelled out though.
For <x> the term that didn't turn to zero was
For <y> the term that didn't go to zero was
Work done for <x>


Work done for <y>

Answers to both <x> and <y> expectation values

Wednesday, February 21, 2018
Notes on Integrals.
These are some notes in case you would like some help with the expectation value related integrals in spherical coordinates.
Tuesday, February 20, 2018
1st Excited States & HW6a due Friday.
Here is a video on the 1st excited states of hydrogen. It includes a HW problem at the end.
HW6:
1a) calculate the expectation value of x for the state discussed in this video, and
b) calculate the expectation values of x for the true sp2-1 state, the one with 1/sqrt(3) and sqrt(2/3) coefficients, as we discussed in class today. (How do they compare. Discuss here in the comments which one is larger as soon as you get results.)
Also, would someone please post those sp2 states, as linear combinations of our s, x, y, z basis states, here soon so everyone can see? Sooner the better. Much appreciated!
2. a) Write the 3 in-plane sp2 states in terms of \(\psi_{2s}, \: \psi_{2px}, \: \psi_{2py}\).
b) Figure out the expectation values of x and y for each state. (Many of the integrals in this problem are, i imagine, equivalent. You can use that. Keeping track of the cross-term coefficients is important too.
c) On an x-y plot, show the location of the expectation value of the vector r for each of the 3 sp2 states.
"Where does those states come from?"
Originally, from solving the wave equation. In that way we find that there are four 1st excited states. Let say they are the four \(\psi_{2,l,m}\) states. Then we use those to construct the 2s, 2px, 2py, 2pz states, which I think provide a better basis. Then we are seeking to make states that are at 120 angles to each other and in the x-y plane, and we do that via linear combinations of the 2s, 2px, 2py, 2pz states. Does that make sense?
HW6:
1a) calculate the expectation value of x for the state discussed in this video, and
b) calculate the expectation values of x for the true sp2-1 state, the one with 1/sqrt(3) and sqrt(2/3) coefficients, as we discussed in class today. (How do they compare. Discuss here in the comments which one is larger as soon as you get results.)
Also, would someone please post those sp2 states, as linear combinations of our s, x, y, z basis states, here soon so everyone can see? Sooner the better. Much appreciated!
2. a) Write the 3 in-plane sp2 states in terms of \(\psi_{2s}, \: \psi_{2px}, \: \psi_{2py}\).
b) Figure out the expectation values of x and y for each state. (Many of the integrals in this problem are, i imagine, equivalent. You can use that. Keeping track of the cross-term coefficients is important too.
c) On an x-y plot, show the location of the expectation value of the vector r for each of the 3 sp2 states.
"Where does those states come from?"
Originally, from solving the wave equation. In that way we find that there are four 1st excited states. Let say they are the four \(\psi_{2,l,m}\) states. Then we use those to construct the 2s, 2px, 2py, 2pz states, which I think provide a better basis. Then we are seeking to make states that are at 120 angles to each other and in the x-y plane, and we do that via linear combinations of the 2s, 2px, 2py, 2pz states. Does that make sense?
Wednesday, February 14, 2018
Homework 5. Metals. Due Monday Feb 19.
1. Consider a 1D metal with dispersion relationship
\(E_k = E_{atom} - 2 \gamma cos(ak)\)
where the hopping integral, \(\gamma\), is 2 eV and E_atom won't really matter.
Values of k range from \(-\pi/a\) to +\(\pi/a\). Let's assume that there is a total of \(10^8 states/cm\) in this 1D band.
a) Show that in the presence of an electric field, the current, J, can be written as \(e (2 \Delta k) v_F\) where \(\Delta k\) refers to the shift in the occupation boundaries due to the applied electric field.
b) Calulate \(v_F\) for the following cases:
i) a 1/8 filled band; ii) a 1/4 filled band; iii) a 1/2 filled band; iv) a 3/4 filled band*(see below for hint)
c) Graph \(v_F\) as a function of \(k_F\). Graph also n, the density of electrons in the conduction band, as a function of \(k_F\). To what extent does \(v_F\) scale with n? Discuss.
d) Calculate \(\Delta k\) for the half-filled band case. Does \(\Delta k\) depend on filling? For the half filled case, what is the total number of electrons in the conduction band and what is the number of electrons the are "unbalanced" and thus participate directly in the net current, J. (email me this number when you get something. or you can post it here for discussion)
2. (Fermi surfaces in 2 dimensions) Consider a 2D metal with dispersion relationship
\(E_k = E_{atom} - 2 \gamma cos(ak_x) - 2 \gamma cos(ak_y)\)
where the hopping integral, \(\gamma\), is 2 eV and E_atom..., well, lets make it zero.
a) At what energy is the bottom of the band? At what value of k does that occur?
b) What is the shape of the Fermi boundary, in k-space, for \(E_F = 0\)? What filling of the band does that correspond to?
c) What is the shape of the Fermi boundary, in k-space, for \(E_F = -2 \gamma \)? What filling of the band does that correspond to? (see hint #2 below if you like)
3. extra credit. With reference to the proceeding problem, what is the shape of the Fermi boundary for the following fillings:
1/8, 1/4, 3/8, 1/2, 3/4, 7/8? What is the Fermi energy for each case?
4. extra credit: For the artificial case in which one uses: \(E_k = \hbar^2 k^2/(2m)\) instead of a valid band dispersion relationship,
a) show that v_f is \(\hbar k_F/m\) and that therefore the current is proportional to
\(e^2 \tau k_F/m\).
b) Write \(k_F\) in terms of n and see what you get for current vs electric field.*(see below)
c) Does the n is this expression come from the number of electrons carrying current or from the Fermi velocity?
\(E_k = E_{atom} - 2 \gamma cos(ak)\)
where the hopping integral, \(\gamma\), is 2 eV and E_atom won't really matter.
Values of k range from \(-\pi/a\) to +\(\pi/a\). Let's assume that there is a total of \(10^8 states/cm\) in this 1D band.
a) Show that in the presence of an electric field, the current, J, can be written as \(e (2 \Delta k) v_F\) where \(\Delta k\) refers to the shift in the occupation boundaries due to the applied electric field.
b) Calulate \(v_F\) for the following cases:
i) a 1/8 filled band; ii) a 1/4 filled band; iii) a 1/2 filled band; iv) a 3/4 filled band*(see below for hint)
c) Graph \(v_F\) as a function of \(k_F\). Graph also n, the density of electrons in the conduction band, as a function of \(k_F\). To what extent does \(v_F\) scale with n? Discuss.
d) Calculate \(\Delta k\) for the half-filled band case. Does \(\Delta k\) depend on filling? For the half filled case, what is the total number of electrons in the conduction band and what is the number of electrons the are "unbalanced" and thus participate directly in the net current, J. (email me this number when you get something. or you can post it here for discussion)
2. (Fermi surfaces in 2 dimensions) Consider a 2D metal with dispersion relationship
\(E_k = E_{atom} - 2 \gamma cos(ak_x) - 2 \gamma cos(ak_y)\)
where the hopping integral, \(\gamma\), is 2 eV and E_atom..., well, lets make it zero.
a) At what energy is the bottom of the band? At what value of k does that occur?
b) What is the shape of the Fermi boundary, in k-space, for \(E_F = 0\)? What filling of the band does that correspond to?
c) What is the shape of the Fermi boundary, in k-space, for \(E_F = -2 \gamma \)? What filling of the band does that correspond to? (see hint #2 below if you like)
3. extra credit. With reference to the proceeding problem, what is the shape of the Fermi boundary for the following fillings:
1/8, 1/4, 3/8, 1/2, 3/4, 7/8? What is the Fermi energy for each case?
4. extra credit: For the artificial case in which one uses: \(E_k = \hbar^2 k^2/(2m)\) instead of a valid band dispersion relationship,
a) show that v_f is \(\hbar k_F/m\) and that therefore the current is proportional to
\(e^2 \tau k_F/m\).
b) Write \(k_F\) in terms of n and see what you get for current vs electric field.*(see below)
c) Does the n is this expression come from the number of electrons carrying current or from the Fermi velocity?
Sunday, February 11, 2018
Metal physics
I am thinking that maybe we could be starting on metal-related physics on Tuesday. Talking about: having the Fermi level in a band, conductivity. the color of copper, and d-level magnetism. Notice how iron and copper are in the same row and not so far apart in the periodic table (26 and 29, respectively). Iron is the quintessential ferromagnet, and copper is a non-magnetic metal with a yellow-orange-red color. Is there some relationship? What role does the Fermi level play in the conductivity, color and magnetism of metals?...
Here is a video for you to watch before Tuesday class which shows the very unusual nature of conductivity in an ordinary metal. The action focuses on very few electrons, all near the Fermi energy and all moving at high velocity.
Notes on \(\Delta k\):
Here is a video for you to watch before Tuesday class which shows the very unusual nature of conductivity in an ordinary metal. The action focuses on very few electrons, all near the Fermi energy and all moving at high velocity.
Notes on \(\Delta k\):
How a solar cell works.
This is a sequence of problems for you to think about and work on.
1. Consider an unbiased pn junction. Suppose a single photon arrives in the depletion region, e.g., around x=0, and suppose it excites one electron from the valence band (top) to the conduction band (bottom). What happens after that? That is, what happens to the electron? What is the primary influence on that electron? Where does that additional electron go?
Think about this wherever you go today. Discuss with people at the beach or downtown or in the forest. Then post your thoughts (as a comment) later tonight.
Hint: You can assume that the recombination time is pretty long compared to other quantum electron time scales and that the electron has time to go somewhere.
More to follow:
1. Consider an unbiased pn junction. Suppose a single photon arrives in the depletion region, e.g., around x=0, and suppose it excites one electron from the valence band (top) to the conduction band (bottom). What happens after that? That is, what happens to the electron? What is the primary influence on that electron? Where does that additional electron go?
Think about this wherever you go today. Discuss with people at the beach or downtown or in the forest. Then post your thoughts (as a comment) later tonight.
Hint: You can assume that the recombination time is pretty long compared to other quantum electron time scales and that the electron has time to go somewhere.
More to follow:
Saturday, February 10, 2018
2nd midterm
Overall, people did well on the midterm. Good work! I am thinking that we could maybe have a second midterm during week 8 or 9, that is somewhere in the range, Feb 27 to March 8.
Sunday, February 4, 2018
Homework 4, due Feb 11.
1. Watch the videos on the biased pn junction. Describe the 6 regions of a biased pn junction. Describe (and discuss) the salient features of each region.
2. Calculate the length scale associated with the recombination region. Do this by solving the differential equation in the 3rd video and thereby finding p(x) for x greater than \(x_d\).
3. Sketch a graph of p(x).
4. Sketch a graph of the hole diffusion current.
Solution notes.
2. Calculate the length scale associated with the recombination region. Do this by solving the differential equation in the 3rd video and thereby finding p(x) for x greater than \(x_d\).
3. Sketch a graph of p(x).
4. Sketch a graph of the hole diffusion current.
Solution notes.
Biased PN Junction videos
This first video provides an overview of the pn junction with an emphasis on the nature of the depletion region. It may help prepare you for the subsequent videos on forward biased junctions. You can skip it if you already understand this part.
Here are the second and third videos (accidentally split into two). These discuss the 6 regions that arise in a biased pn junction (normal p, recombination, depleted p, depleted n, recombination, normal n). Recombination and a minority carrier diffusion current occur together outside the depletion region in a "recombination region". For HW, calculate and discuss the length scale associated with the recombination region. Is larger or smaller than the length scale of the depletion region, \(x_d\)?
Here are the second and third videos (accidentally split into two). These discuss the 6 regions that arise in a biased pn junction (normal p, recombination, depleted p, depleted n, recombination, normal n). Recombination and a minority carrier diffusion current occur together outside the depletion region in a "recombination region". For HW, calculate and discuss the length scale associated with the recombination region. Is larger or smaller than the length scale of the depletion region, \(x_d\)?
Subscribe to:
Comments (Atom)
